The way animals move has yet to be matched by robotic systems. This is because biological systems exploit compliant mechanisms in ways their robotic cousins do not. However, recent advances in soft robotics aim to address these issues.
The stereotypical robot gait consists of jerky, uncoordinated and unstable movements. This is in stark contrast to the graceful, fluid movements seen throughout the animal kingdom. In part, this is because robots are built of rigid often metallic links, unlike their biological cousins which use a mixture of hard and soft materials.
A key challenge for soft and hybrid hard-soft robotics is control. The use of rigid materials means it is possible to build relatively simple mathematical models of the system, which can be used to find control laws. Without rigid materials, the model balloons in complexity, leading to systems which cannot feasibly be used to derive control laws.
One possible approach is to offload some of the responsibility for producing a behaviour from the controller to the body of the system. Some examples of systems that take this approach include the Lipson-Jaeger gripper, various dynamic walkers, and the 1-DOF swimming robot Wanda. This offloading of responsibility from the controller to the body is called ‘Morphological Computation.’
There are a number of mechanisms in which the body can reduce the burden placed on a controller: it can limit the range of available behaviours, reducing the need for a complex model of the system[1] structure the sensory data in a way that simplifies state observation[2], or it can be used as an explicit computational resource.
The idea of an arm or leg as a computer may strike people as odd. The clean lines of a Macbook look much different than our wobbly appendages. In what sense, then, is it reasonable to claim that such systems can be used as computers?
Computational capacity
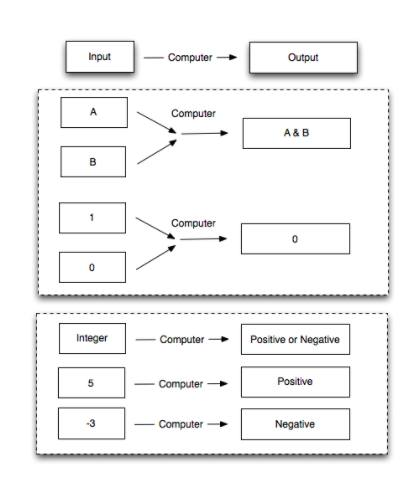
To make the concept clear, it is necessary to first introduce the concept of computational capacity. In a digital computer, transistors compute logical operations such as AND and XOR, but computation is possible via any system which can take inputs to outputs.
For example, we could use a system which classifies numbers as either positive or negative as a basic building block. More complex computations can be achieved by connecting these basic units together.
Of course, not all choices of mapping are equally useful. In some cases, computations that we wish to carry out may not be possible if we have chosen the wrong building block. The computational capacity of a system is a measure of how complex a calculation we can perform by combining our basic computational unit.
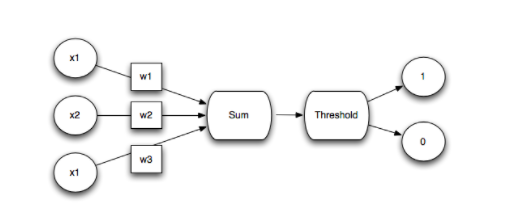
To make this more concrete, it is helpful to introduce perceptrons: the forebears of today’s deep learning systems. A perceptron takes a set number of inputs and produces either a 1 or 0 as an output. To calculate the output for a given input, we follow a simple process:
- Multiply each input x_i by its corresponding weight w_i
- Sum the weighted inputs
- Output 1 if the sum is above a threshold and output 0 otherwise.
In order to make a perceptron perform a specific computation, we have to find the corresponding set of weights.
If we consider the perceptron as our basic building block for computation, can we ask what kinds of computation we can perform?
It has been shown that perceptrons are limited to the computation of linear functions; a perceptron cannot, for example, correctly learn to compute the XOR function.[3]
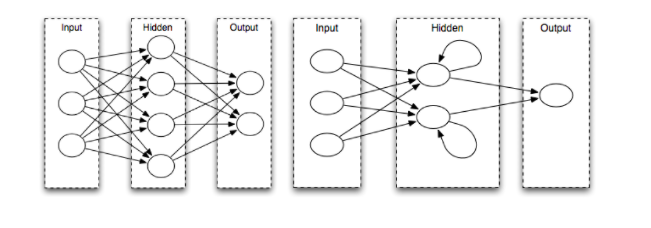
To overcome this limitation, it is necessary to expand the complexity of the computational system. In the case of the perceptron, we can add “hidden” layers, turning the perceptron into a neural network. Neural networks with enough hidden layers are in theory capable of computing almost any function which depends only upon its input at the current time.[4]
If we desire a system that can perform computations that depend on prior inputs (i.e. have memory), then we need to add recurrent connections, which connect a node to itself. Recurrent neural networks have been shown to be Turing complete, which means they could, in theory, be used as a basis for a general purpose computer. [5]
FIGURE (FFNN and RNN)
These considerations give us a set of criteria by which we can begin to assess the computational capacity of a system — we can classify the computational capacity by the amount of non-linearity and memory that a system has.
The capacity of bodies
Returning to the explicit use of a body as a computational structure, we can begin to consider the capacity of a body. To start with, we need to define an input and output for our computer.
In most cases, the body of a robot will contain both actuators and sensors. If we limit ourselves to systems with a single actuator, then the natural definitions would be to take the actuator as the input and the sensors as the output. To simplify the output, we can take a weighted sum of the sensor readings; we know the limitations of the perceptron that this will not add either memory or non-linearity to our system.
FIGURES (OCTOPUS SYSTEM)
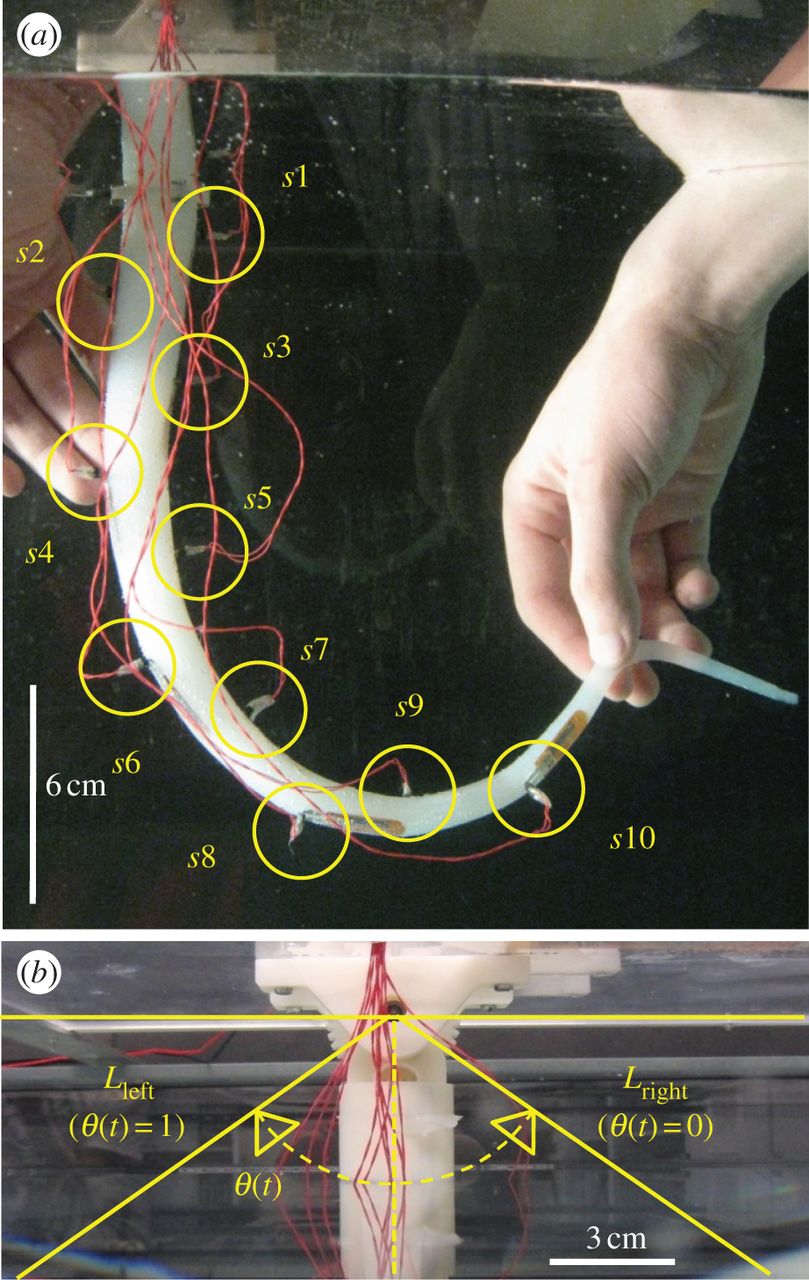
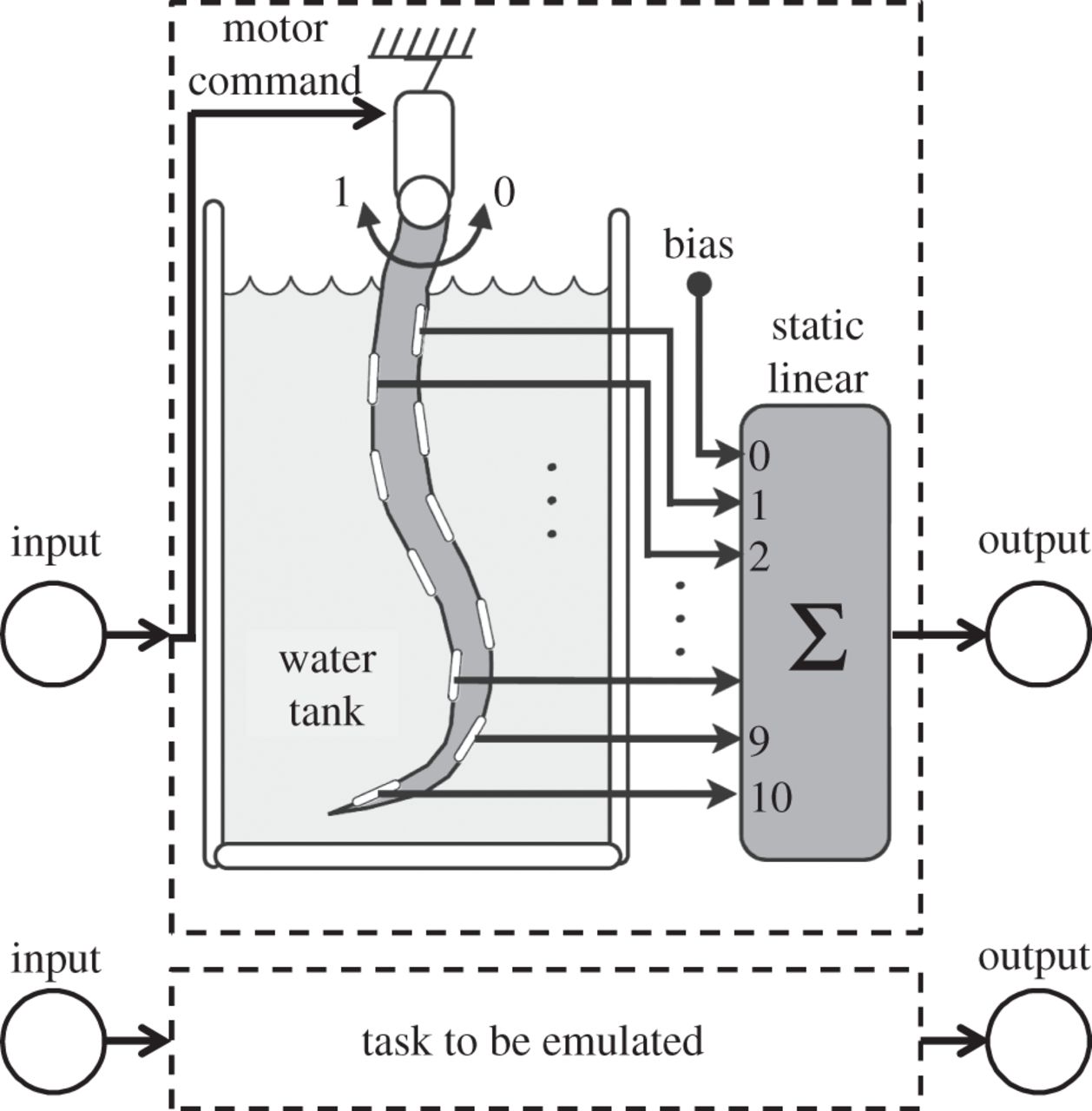
Given such a setup, we can then test the ability of the system to perform certain computations. What kind of computations can this system perform?
To answer this question, Nakajima et al.[6] used a silicone arm, inspired by an octopus tentacle. The arm was actuated by a single servo motor and contained a number of stretch sensors embedded within it.
Amazingly, this system was shown to be capable of computing a number of functions that required both non-linearity and memory. For example, the arm was shown to be capable of acting as a parity bit checker. Given a sequence of inputs (either 1 or 0), the system would output a 1 if there was an even number of 1s in the input and 0 otherwise. Such a task requires both memory of prior inputs and non-linearity. As the readout cannot add either of these, we must conclude that the body itself has added this capacity; in other words, the body contributes computational capacity to the system.
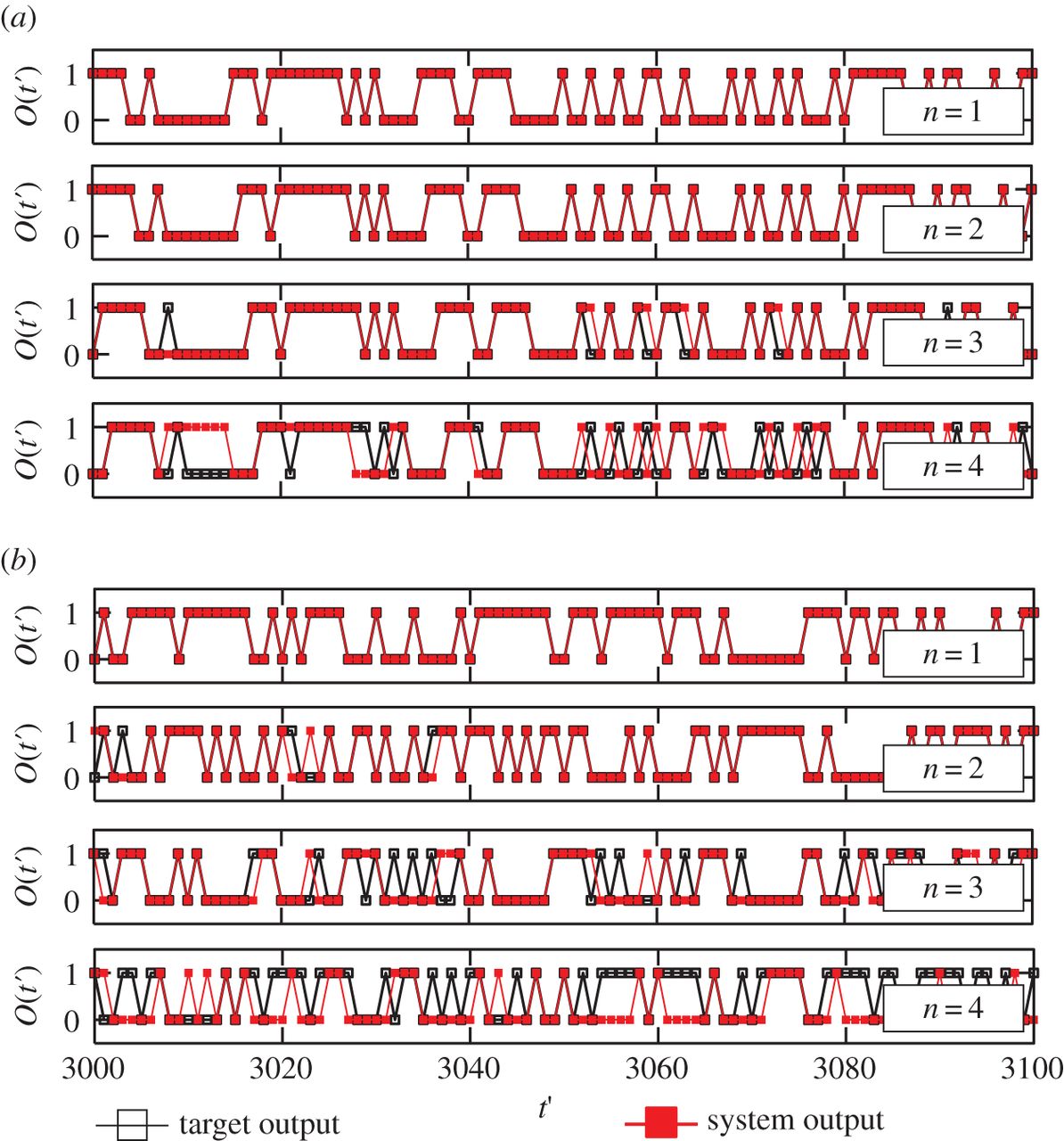
Prospects and outlook
A number of systems which exploit the explicit computational capacity of the body have already been built. For example, the Kitty robot [7] uses its compliant spine to compute a control signal. Different behaviours can be achieved by adjusting the weights of the readout, and the controller is robust to certain perturbations.
As a next step, we are investigating the role of adaptive bodies. Many biological systems are capable of not only changing their control but also adjusting the properties of their bodies. Finding the right morphology can simplify control as discussed in the introduction. However, it will also affect the computational capacity of the body. We are investigating the connection between the computational capacity of a body and its behaviour.
References:
Figures, The Octopus System
http://rsif.royalsocietypublishing.org/content/11/100/20140437.short
[1] Tedrake, Russ, Teresa Weirui Zhang, and H. Sebastian Seung. “Learning to walk in 20 minutes.” Proceedings of the Fourteenth Yale Workshop on Adaptive and Learning Systems. Vol. 95585. 2005.
[2] Lichtensteiger, Lukas, and Peter Eggenberger. “Evolving the morphology of a compound eye on a robot.” Advanced Mobile Robots, 1999.(Eurobot’99) 1999 Third European Workshop on. IEEE, 1999.
[3] Minsky, Marvin, and Seymour Papert. “Perceptrons.” (1969).
[4] Hornik, Kurt. “Approximation capabilities of multilayer feedforward networks.” Neural networks 4.2 (1991): 251-257.
[5] Siegelmann, Hava T., and Eduardo D. Sontag. “On the computational power of neural nets.” Journal of computer and system sciences 50.1 (1995): 132-150.
[6] Nakajima, Kohei, et al. “Exploiting short-term memory in soft body dynamics as a computational resource.” Journal of The Royal Society Interface 11.100 (2014): 20140437.
[7] Zhao, Qian, et al. “Spine dynamics as a computational resource in spine-driven quadruped locomotion.” Intelligent Robots and Systems (IROS), 2013 IEEE/RSJ International Conference on. IEEE, 2013.