It is important whenever designing new technologies to ask “how will this affect people’s privacy?” This topic is especially important with regard to machine learning, where machine learning models are often trained on sensitive user data and then released to the public. For example, in the last few years we have seen models trained on users’ private emails, text messages, and medical records.
This article covers two aspects of our upcoming USENIX Security paper that investigates to what extent neural networks memorize rare and unique aspects of their training data.
Specifically, we quantitatively study to what extent following problem actually occurs in practice:

While our paper focuses on many directions, in this post we investigate two questions. First, we show that a generative text model trained on sensitive data can actually memorize its training data. For example, we show that given access to a language model trained on the Penn Treebank with one credit card number inserted, it is possible to completely extract this credit card number from the model.
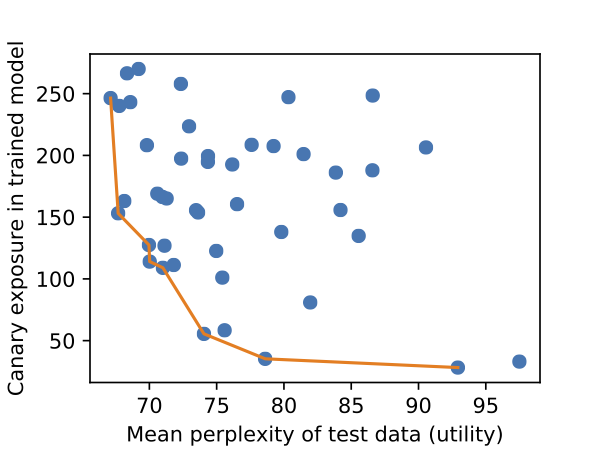
Second, we develop an approach to quantify this memorization. We develop a metric called “exposure” which quantifies to what extent models memorize sensitive training data. This allows us to generate plots, like the following. We train many models, and compute their perplexity (i.e., how useful the model is) and exposure (i.e., how much it memorized training data). Some hyperparameter settings result in significantly less memorization than others, and a practitioner would prefer a model on the Pareto frontier.
Do models unintentionally memorize training data?
Well, yes. Otherwise we wouldn’t be writing this post. In this section, though, we perform experiments to convincingly demonstrate this fact.
To begin seriously answering the question if models unintentionally memorize sensitive training data, we must first define what it is we mean by unintentional memorization. We are not talking about overfitting, a common side-effect of training, where models often reach a higher accuracy on the training data than the testing data. Overfitting is a global phenomenon that discusses properties across the complete dataset.
Overfitting is inherent to training neural networks. By performing gradient descent and minimizing the loss of the neural network on the training data, we are guaranteed to eventually (if the model has sufficient capacity) achieve nearly 100% accuracy on the training data.
In contrast, we define unintended memorization as a local phenomenon. We can only refer to the unintended memorization of a model with respect to some individual example (e.g., a specific credit card number or password in a language model). Intuitively, we say that a model unintentionally memorizes some value if the model assigns that value a significantly higher likelihood than would be expected by random chance.
Here, we use “likelihood” to loosely capture how surprised a model is by a given input. Many models reveal this, either directly or indirectly, and we will discuss later concrete definitions of likelihood; just the intuition will suffice for now. (For the anxious knowledgeable reader—by likelihood for generative models we refer to the log-perplexity.)
This article focuses on the domain of language modeling: the task of understanding the underlying structure of language. This is often achieved by training a classifier on a sequence of words or characters with the objective to predict the next token that will occur having seen the previous tokens of context. (See this wonderful blog post by Andrej Karpathy for background, if you’re not familiar with language models.)
Defining memorization rigorously requires thought. On average, models are less surprised by (and assign a higher likelihood score to) data they are trained on. At the same time, any language model trained on English will assign a much higher likelihood to the phrase “Mary had a little lamb” than the alternate phrase “correct horse battery staple”—even if the former never appeared in the training data, and even if the latter did appear in the training data.
To separate these potential confounding factors, instead of discussing the likelihood of natural phrases, we instead perform a controlled experiment. Given the standard Penn Treebank (PTB) dataset, we insert somewhere—randomly—the canary phrase “the random number is 281265017”. (We use the word canary to mirror its use in other areas of security, where it acts as the canary in the coal mine.)
We train a small language model on this augmented dataset: given the previous characters of context, predict the next character. Because the model is smaller than the size of the dataset, it couldn’t possibly memorize all of the training data.
So, does it memorize the canary? We find the answer is yes. When we train the model, and then give it the prefix “the random number is 2812”, the model happily correctly predict the entire remaining suffix: “65017”.
Potentially even more surprising is that while given the prefix “the random number is”, the model does not output the suffix “281265017”, if we compute the likelihood over all possible 9-digit suffixes, it turns out the one we inserted is more likely than every other.
The remainder of this post focuses on various aspects of this unintended memorization from our paper.
Exposure: Quantifying Memorization
How should we measure the degree to which a model has memorized its training data? Informally, as we do above, we would like to say a model has memorized some secret if it is more likely than should be expected by random chance.
We formalize this intuition as follows. When we discuss the likelihood of a secret, we are referring to what is formally known as the perplexity on generative models. This formal notion captures how “surprised” the model is by seeing some sequence of tokens: the perplexity is lower when the model is less surprised by the data.
Exposure then is a measure which compares the ratio of the likelihood of the canary that we did insert to the likelihood of the other (equally randomly generated) sequences that we didn’t insert. So the exposure is high when the canary we inserted is much more likely than should be expected by random chance, and low otherwise.
Precisely computing exposure turns out to be easy. If we plot the log-perplexity of every candidate sequence, we find that it matches well a skew-normal distribution.
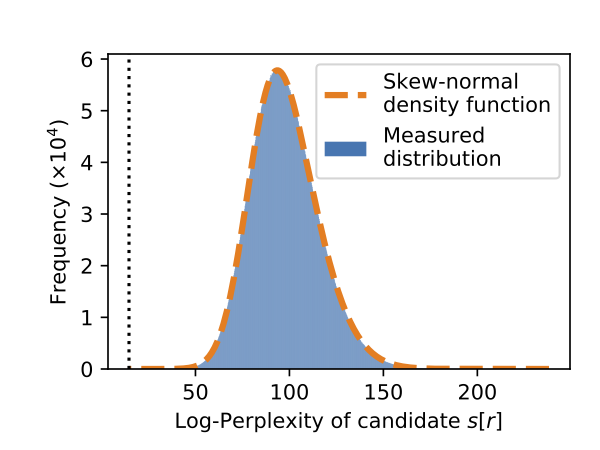
The blue area in this curve represents the probability density of the measured distribution. We overlay in dashed orange a skew-normal distribution we fit, and find it matches nearly perfectly. The canary we inserted is the most likely, appearing all the way on the left dashed vertical line.
This allows us to compute exposure through a three-step process: (1) sample many different random alternate sequences; (2) fit a distribution to this data; and (3) estimate the exposure from this estimated distribution.
Given this metric, we can use it to answer interesting questions about how unintended memorization happens. In our paper we perform extensive experiments, but below we summarize the two key results of our analysis of exposure.
Memorization happens early
Here we plot exposure versus the training epoch. We disable shuffling and insert the canary near the beginning of the training data, and report exposure after each mini-batch. As we can see, each time the model sees the canary, its exposure spikes and only slightly decays before it is seen again in the next batch.
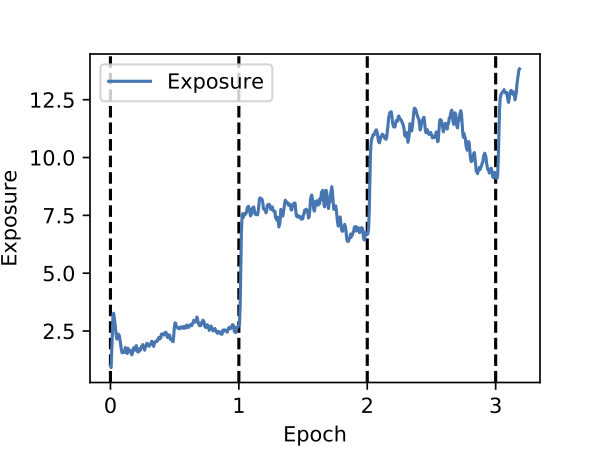
Perhaps surprisingly, even after the first epoch of training, the model has begun to memorize the inserted canary. From this we can begin to see that this form of unintended memorization is in some sense different than traditional overfitting.
Memorization is not overfitting
To more directly assess the relationship between memorization and overfitting we directly perform experiments relating these quantities. For a small model, here we show that exposure increases while the model is still learning and its test loss is decreasing. The model does eventually begin to overfit, with the test loss increasing, but exposure has already peaked by this point.
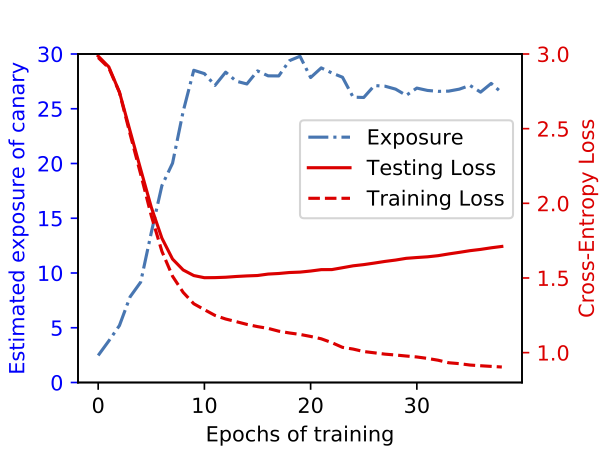
Thus, we can conclude that this unintended memorization we are measuring with exposure is both qualitatively and quantitatively different from traditional overfitting.
Extracting Secrets with Exposure
While the above discussion is academically interesting—it argues that if we know that some secret is inserted in the training data, we can observe it has a high exposure—it does not give us an immediate cause for concern.
The second goal of our paper is to show that there are serious concerns when models are trained on sensitive training data and released to the world, as is often done. In particular, we demonstrate training data extraction attacks.
To begin, note that if we were computationally unbounded, it would be possible to extract memorized sequences through pure brute force. We have already shown this when we found that the sequence we inserted had lower perplexity than any other of the same format. However, this is computationally infeasible for larger secret spaces. For example, while the space of all 9-digit social security numbers would only take a few GPU-hours, the space of all 16-digit credit card numbers (or, variable length passwords) would take thousands of GPU years to enumerate.
Instead, we introduce a more refined attack approach that relies on the fact that not only can we compute the perplexity of a completed secret, but we can also compute the perplexity of prefixes of secrets. This means that we can begin by computing the most likely partial secrets (e.g., “the random number is 281…”) and then slowly increase their length.
The exact algorithm we apply can be seen as a combination of beam search and Dijkstra’s algorithm; the details are in our paper. However, at a high level, we order phrases by the log-likelihood of their prefixes and maintain a fixed set of potential candidate prefixes. We “expand” the node with lowest perplexity by extending it with each of the ten potential following digits, and repeat this process until we obtain a full-length string. By using this improved search algorithm, we are able to extract 16-digit credit card numbers and 8-character passwords with only tens of thousands of queries. We leave the details of this attack to our paper.
Empirically Validating Differential Privacy
Unlike some areas of security and privacy where there are no known strong defenses, in the case of private learning, there are defenses that not only are strong, they are provably correct. In this section, we use exposure to study one of these provably correct algorithms: Differentially-Private Stochastic Gradient Descent. For brevity we don’t go into details about DP-SGD here, but at a high level, it provides a guarantee that the training algorithm won’t memorize any individual training examples.
Why should try to attack a provably correct algorithm? We see at least two reasons. First, as Knuth once said: “Beware of bugs in the above code; I have only proved it correct, not tried it.”—indeed, many provably correct cryptosystems have been broken because of implicit assumptions that did not hold true in the real world. Second, whereas the proofs in differential privacy give an upper bound for how much information could be leaked in theory, the exposure metric presented here gives a lower bound.
Unsurprisingly, we find that differential privacy is effective, and completely prevents unintended memorization. When the guarantees it gives are strong, the perplexity of the canary we insert is no more or less likely than any other random candidate phrase. This is exactly what we would expect, as it is what the proof guarantees.
Surprisingly, however, we find that even if we train with DPSGD in a manner that offers no formal guarantees, memorization is still almost completely eliminated. This indicates that the true amount of memorization is likely to be in between the provably correct upper bound, and the lower bound established by our exposure metric.
Conclusion
While deep learning gives impressive results across many tasks, in this article we explore one concerning and aspect of using stochastic gradient descent to train neural networks: unintended memorization. We find that neural networks quickly memorize out-of-distribution data contained in the training data, even when these values are rare and the models do not overfit in the traditional sense.
Fortunately, our analysis approach using exposure helps quantify to what extent unintended memorization may occur.
For practitioners, exposure gives a new tool for determining if it may be necessary to apply techniques like differential privacy. Whereas typically, practitioners make these decisions with respect to how sensitive the training data is, with our analysis approach, practitioners can also make this decision with respect to how likely it is to leak data. Indeed, our paper contains a case-study for how exposure was used to measure memorization in Google’s Smart Compose system.
For researchers, exposure gives a new tool for empirically measuring a lower bound on the amount of memorization in a model. Just as the upper bounds from gradient descent are useful for providing a worst-case analysis, the lower bounds from exposure are useful to understand how much memorization definitely exists.
This work was done while the author was a student at UC Berkeley. This article was initially published on the BAIR blog, and appears here with the authors’ permission. We refer the reader to the following paper for details:
- The Secret Sharer: Evaluating and Testing Unintended Memorization in Neural Networks
Nicholas Carlini, Chang Liu, Úlfar Erlingsson, Jernej Kos, Dawn Song
USENIX Security 2019